Learning classifier systems (LCS) and Genetics-Based Machine Learning (GBML) have been using the multiplexer problem as a toy problem because of its properties; among others, its dynamic dependencies based on the input values and the exponential nature of the required solution as a function of the number of inputs. There is a great introduction why the multiplexer is interesting for LCS and GBML systems at Wilson’s XCS field-defining paper.
A simple definition [1] of the multiplexer is as follows:
Multiplexing is the generic term used to describe the operation of sending one or more analogue or digital signals over a common transmission line at different times or speeds and as such, the device we use to do just that is called a Multiplexer.
A simple graphical representation of the 6 input (2 addresses + 4 lines) multiplexer as provided in [1] is shown below.
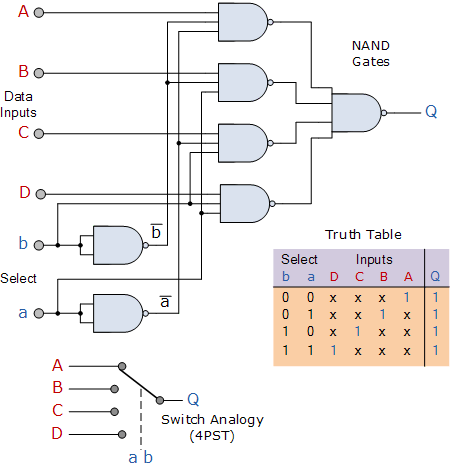
Let’s try to learn the solution by evolving it using Genetic Programming [2] as originally presented by John Koza.
Choosing a framework
To solve the problem we are not going to implement Koza’s initial genetic programming code from scratch. Instead we are going to do it by using DEAP [3], evolutionary computation framework for rapid prototyping and testing of ideas. DEAP is written in Python and you can just us it in a Jupiter notebook [4].
Problem definition
Imagine you have the problem defined in a CSV file. Each row is a possible input combination to the problem illustrated above. A0 and A1 represent the two address lines on the 6 input multiplexer. I0, I1, I2 and A3 the selectable lines based on the values of the address lines. Finally, O is the expected output.
| A0 | A1 | I0 | I1 | I2 | I3 | O |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 1 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Imagine you have the above data stored in a file name mux-2-4.csv. You could load it as follows:
import csv
filename = "mux-2-4.csv"
problem_examples = open(filename)
reader = csv.reader(problem_examples)
raw = [row for row in reader]
names = raw[0]
problem = [list(map(lambda x: x == '1', instance)) for instance in raw[1:]]
Choosing the right operators
The first decision we have to make is what operators are we going to use to define the space of individuals we want to evolve.
import operator
import itertools
import deap
# Define a new primitive set for strongly typed GP.
pset = gp.PrimitiveSetTyped("MAIN", itertools.repeat(bool, 6), bool, "IN")
# Boolean operators.
pset.addPrimitive(operator.and_, [bool, bool], bool)
pset.addPrimitive(operator.or_, [bool, bool], bool)
pset.addPrimitive(operator.not_, [bool], bool)
# Logic operators.
# Define a new if-then-else function
def if_then_else(input, output1, output2):
if input: return output1
else: return output2
pset.addPrimitive(if_then_else, [bool, bool, bool], bool)
pset.addTerminal(False, bool)
pset.addTerminal(True, bool)
As you can see above, we just choose to add three basic Boolean algebra operators (and, or and not) as well as an if_then_else operator. This together with eight terminals (the six input ones plus True and _False) form the set of primitives we will use. One nifty property of DEAP is that allows you to use strongly type GP. In this example may not be very relevant, however, if your problem deals with different types of terminals, this would guarantee your programs would be type correct.
The GP algorithm composition and params
The next step is simple. Just define the algorithm you want to run and also add the required params.
from deap import base
from deap import creator
from deap import tools
from deap import gp
creator.create("FitnessMax", base.Fitness, weights=(1.0,))
creator.create("Individual", gp.PrimitiveTree, fitness=creator.FitnessMax)
toolbox = base.Toolbox()
toolbox.register("expr", gp.genHalfAndHalf, pset=pset, min_=2, max_=4)
toolbox.register("individual", tools.initIterate, creator.Individual, toolbox.expr)
toolbox.register("population", tools.initRepeat, list, toolbox.individual)
toolbox.register("compile", gp.compile, pset=pset)
def evalProblem(individual):
# Transform the tree expression in a callable function.
func = toolbox.compile(expr=individual)
# Evaluate the sum of correctly classified examples.
# In this case 64 will be the maximum score for the 6-input multiplexer.
result = sum(bool(func(*ins[:6])) is ins[6] for ins in problem)
return result,
toolbox.register("evaluate", evalProblem)
toolbox.register("select", tools.selDoubleTournament, fitness_size=3, parsimony_size=1.1, fitness_first=True)
toolbox.register("mate", gp.cxOnePoint)
toolbox.register("expr_mut", gp.genFull, min_=2, max_=4)
toolbox.register("mutate", gp.mutUniform, expr=toolbox.expr_mut, pset=pset)
toolbox.decorate("mate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5))
toolbox.decorate("mutate", gp.staticLimit(key=operator.attrgetter("height"), max_value=5))
Collecting statistics
DEAP allows you to collect a variety of statistics. Here we will just show some of the basic ones. More than enough for this example.
import numpy
from deap import algorithms
def run():
pop = toolbox.population(n=500)
hof = tools.HallOfFame(1)
stats = tools.Statistics(lambda ind: ind.fitness.values)
stats.register("avg", numpy.mean)
stats.register("std", numpy.std)
stats.register("min", numpy.min)
stats.register("max", numpy.max)
algorithms.eaSimple(pop, toolbox, 0.5, 0.1, 25, stats, halloffame=hof)
return pop, stats, hof
Let it run
Finally, the last thing we need to do is just run the algorithm we put together.
import random
random.seed(10)
pop, stats, hof = run()
If everything goes as expected, you should get an output along the lines below.
gen nevals avg std min max
0 500 32.992 5.41479 16 48
1 282 36.66 4.79754 16 48
2 278 39.096 3.94142 24 48
3 276 40.216 4.04343 22 48
4 266 41.632 3.38889 24 48
5 255 42.472 3.579 24 52
6 251 43.534 3.04907 28 50
7 283 43.718 3.38504 30 50
8 259 44.316 3.81158 24 50
9 277 44.832 4.07772 28 52
10 281 45.53 4.01611 24 56
11 264 46.154 4.12047 24 56
12 261 46.984 4.46629 24 56
13 270 47.87 4.29803 24 58
14 251 48.81 4.50621 30 58
15 277 49.84 4.57498 26 60
16 304 50.25 5.0223 24 60
17 290 51.464 4.8831 32 60
18 267 52.188 5.52564 32 60
19 254 53.232 5.92538 20 60
20 266 54.06 5.58573 28 64
21 289 54.294 5.79099 24 64
22 270 55.222 5.3711 32 64
23 281 56.194 4.93927 34 64
24 282 56.616 5.53286 31 64
25 296 57.462 5.29647 36 64
And as you can see from the output, our simple algorithm was able to solve the problem correctly for all the 64 instances we provided in our training data.
What did we get?
DEAP’s run returned the best individual found during the experiment. DEAP provides data in DOT format for each individual. DOT if the format GraphViz [5] uses to express graphs. If you plot the tree for the best individual you get the graph below. Remember that we defined IN0, IN1, IN2, IN3, IN4, IN5 to map to the original notation A0, A1, I0, I1, I2, I3.
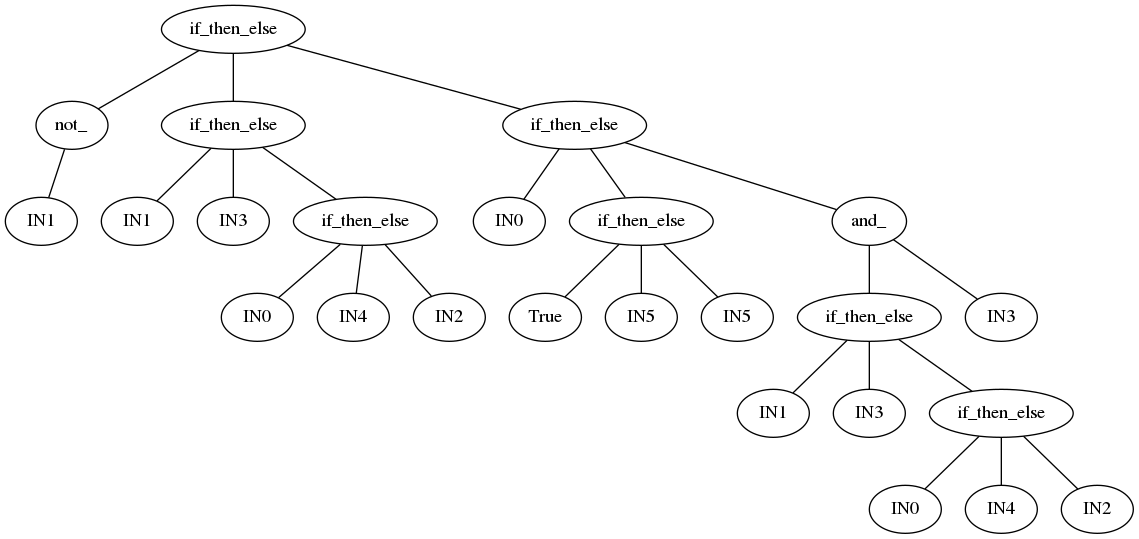
This simple example illustrates how you can actually evolve a simple human-readable solution to the challenge of learning the multiplexer problem. This approach is usually referred as symbolic regression [6]. It also shows you can actually solved with a subset of the operators we provided.
References
[1] https://www.electronics-tutorials.ws/combination/comb_2.html
[2] http://geneticprogramming.com